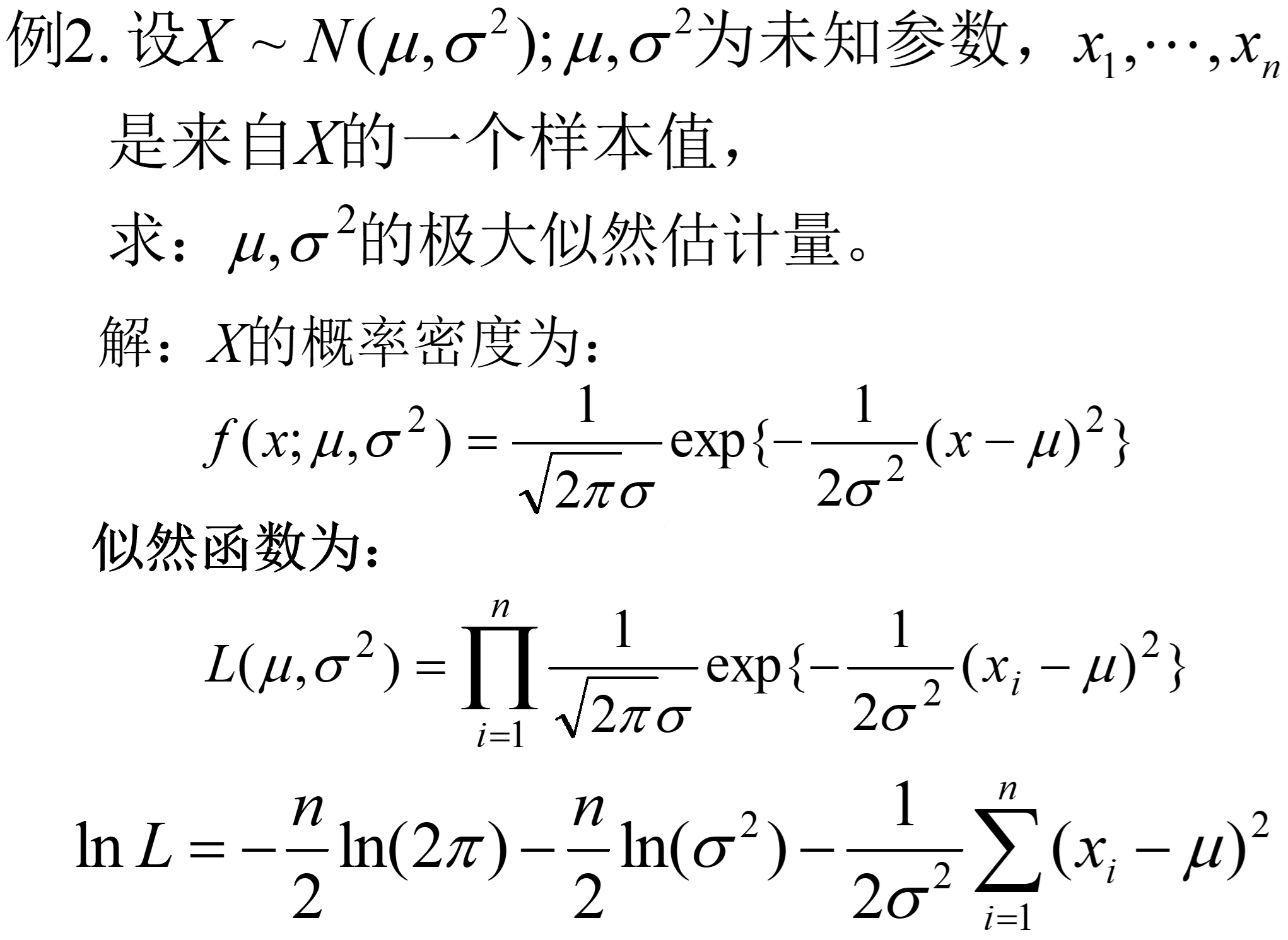【参数估计】点估计

1 前言

参数估计本质上是用样本推测整体，具体而言是使用样本的观测值来对已知模型的未知参数进行估计

2 矩估计

矩估计基于样本矩对总体矩进行估计，其基本原理为样本矩在一定程度上可以逼近总体矩

当有个参数需要进行估计时，可以根据样本观测值的阶矩列出个方程，并进行求解

为了计算简单，通常情况下会用相对低阶的矩，例如样本的均值（一阶原点矩）和方差（二阶中心矩）去估计总体的期望和方差

矩估计仅适用于样本矩存在的情况

2.1 基本概念

2.2 解题步骤

一般情况下矩估计的步骤：

这里的代表根据分布计算出来的期望，即基本概念中的

这里的代表根据样本观测值计算出的均值，即基本概念中的

2.3 例题

解答如下

3 极大似然估计

3.1 基本概念

先说比较直观的理解：若一随机试验有多个可能结果，现在做一次试验，结果A发生，而导致结果A发生的原因有很多，在分析导致A发生的原因时，将使得结果A发生的概率最大的原因推断为真实原因。注意：推断出来的原因不一定是实际上的真实原因，只是“看起来最像”

即在一次抽样中，若得到观测值，则选取作为的估计值，使得当时，样本出现的概率最大

从上述定义出发，引入似然性 (likelihood) 与概率 (possibility) 的区别：

• 概率 是在已知参数的情况下，发生观测结果可能性大小
• 似然性则是从观测结果出发，分布函数的参数为的可能性大小

3.2 解题步骤

极大似然估计（Maximum Likelihood Estimation, MLE）的一般步骤：

1. 由总体导出样本的联合分布律（或联合密度）
2. 把样本联合分布律（或联合密度）中自变量看成已知参数，而把参数看作自变量，得到似然函数
3. 求似然函数的最大值点（一般用求导方式求解，常常转化为求的最大值点），即的MLE
4. 在最大值点的表达式中，用样本值带入可得参数的极大似然估计值

似然函数的构造：

对于离散型随机变量 对于连续型随机变量 其中为连续型随机变量的概率密度（PDF），由于不随参数变化而变化，股上式可重写为

3.3 例题